Goldbach's weak conjecture
In number theory, Goldbach's weak conjecture, also known as the odd Goldbach conjecture, the ternary Goldbach problem, or the 3-primes problem, states that:
- Every odd number greater than 7 can be expressed as the sum of three odd primes. (A prime may be used more than once in the same sum.)
This conjecture is called "weak" because if Goldbach's strong conjecture (concerning sums of two primes) is proven, it would be true. (Since if every even number greater than 4 is the sum of two odd primes, merely adding 3 to each even number greater than 4 will produce the odd numbers greater than 7.)
The conjecture has not yet been proven, but there have been some useful near misses. In 1923, Hardy and Littlewood showed that, assuming the generalized Riemann hypothesis, the odd Goldbach conjecture is true for all sufficiently large odd numbers. In 1937, Ivan Matveevich Vinogradov eliminated the dependency on the generalised Riemann hypothesis and proved directly (see Vinogradov's theorem) that all sufficiently large odd numbers can be expressed as the sum of three primes. Vinogradov's original proof, as it used the ineffective Siegel–Walfisz theorem, did not give a bound for "sufficiently large", his student K. Borozdin proved, in 1939, that 314348907 is large enough. This number has 6,846,169 decimal digits, so checking every number under this figure would be highly infeasible with current technology.
In 2002, Liu Ming-Chit (University of Hong Kong) and Wang Tian-Ze lowered this threshold to approximately 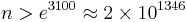 . The exponent is still much too large to admit checking all smaller numbers by computer. (Computer searches have only reached as far as
. The exponent is still much too large to admit checking all smaller numbers by computer. (Computer searches have only reached as far as 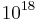 for the strong Goldbach conjecture, and not much further than that for the weak Goldbach conjecture.) However, this bound is small enough that any single odd number below the bound can be verified by existing primality tests such as elliptic curve primality proving, which generates a proof of primality and has been used on numbers with as many as 26,643 digits.[1]
for the strong Goldbach conjecture, and not much further than that for the weak Goldbach conjecture.) However, this bound is small enough that any single odd number below the bound can be verified by existing primality tests such as elliptic curve primality proving, which generates a proof of primality and has been used on numbers with as many as 26,643 digits.[1]
In 1997, Deshouillers, Effinger, te Riele and Zinoviev showed[2] that the generalized Riemann hypothesis implies Goldbach's weak conjecture for all numbers. This result combines a general statement valid for numbers greater than 1020 with an extensive computer search of the small cases.
Leszek Kaniecki showed every odd integer is a sum of at most five primes, under Riemann Hypothesis. [3]
References
- ^ N. Lygeros, F. Morain, O. Rozier. http://www.lix.polytechnique.fr/~morain/Primes/myprimes.html.
- ^ Deshouillers, Effinger, Te Riele and Zinoviev (1997). "A complete Vinogradov 3-primes theorem under the Riemann hypothesis" (PDF). Electronic Research Announcements of the American Mathematical Society 3 (15): 99–104. doi:10.1090/S1079-6762-97-00031-0. http://www.ams.org/era/1997-03-15/S1079-6762-97-00031-0/S1079-6762-97-00031-0.pdf.
- ^ Kaniecki, Leszek (1995). "On Šnirelman's constant under the Riemann hypothesis". Acta Arithmetica 4: pp. 361–374